Bir kağıt ve bir makasla neler yapılabilir? Yanına bir de taş koyarsanız oyun oynanabilir. Taş, makas, kağıt oyunu. Peki ya size tek bir kesikle istediğiniz her şeyi yapabileceğinizi söylesem? Tek bir makas kesiğiyle beyaz bir kağıdın içinde saklı güzel bir kuğuyu ortaya çıkartabilirsiniz. Nasıl yaptığımı göstereceğim merak etmeyin. Önce işin matematiğinden daha doğrusu geometrisinden başlayalım.
Düz bir kağıdın ortasından çıkartabileceğiniz en basit şekil ne olabilir? Bir kare değil mi? Peki bu kareyi kesebilmek için ne yaparsınız? Makasla ortasına bir dalıp, sonra da etrafını düzeltmeye çalışırsınız… En azından benim ilk aklıma gelen yöntem bu. Fakat sonra düşününce -daha doğrusu matematikçi doktor Katie Steckles ile tanışınca – kağıdı katlayıp kesme fikri ortaya çıktı. Bu daha pratik bir yöntem gibi gözüküyor. Kareyi ikiye katlarsak ne olur? İki dikdörtgen ortaya çıkar. Ve o dikdörtgeni kesmek, kağıdın ortasına makasla dalıp kesmeye çalışmaktan çok daha kolay ve medeni. Peki daha da kolaylaştırılabilir mi? Kağıdı bir kez katlayan, iki kez de katlar. Katlarsa bu kez dört kare ortaya çıkar. Ve bu kareleri kesmek dikdörtgenleri kesmekten daha kolay hale gelir. İki hamlede işlem tamam. Peki tek bir makas kesiğiyle kare nasıl yapılabilir? Bir kere daha katlarız.
Bu noktaya gelinceye kadar takip ettiğimiz düşünce silsilesindeki gelişimi fark ettiniz mi? Önce 1 kez katlayıp 3 kez kestik. Sonra 2 kez katlayıp 2 kez kestik. En sonunda 3 kez katlayınca 1 seferde keserek kare şeklini oluşturmayı başardık. Yaptığımız bu işlemi formülize etmeye çalışalım. 1 Kat 3 Kes. 2 Kat 2 Kes. 3 Kat 1 Kes. Katlama sayısı arttıkça kesme sayısı azalıyor. Buradan yola çıkarak şöyle bir şey diyebilir miyiz? Eğer bir kağıdı yeterince katlarsak 1 kesikte ona istediğimiz şekli verebiliriz. “Yaşasın yeni bir keşif yaptık!” Ne diyelim buna? Bu sonuca bir kağıdı katlayıp keserek ulaştığımıza göre mesela “katla ve kes teoremi” diyelim mi? Diyelim demesine ama bizden önce başkaları da keşfetmiş olabilir Geçen haftaki videomda anlattığım çoklu keşfin bir örneğini yaşamış olduk böylece.
Şaka bir yana kesilecek şeklin düz kenarlardan oluşması kaydıyla gerçekten de bu bilimsel önermemiz doğru. Katla ve Kes Teoremine göre düz kenarlara sahip her geometrik şekil uygun bir katlama ve tek bir kesikle oluşturulabilir. Her geometrik şekil. Şeklin içinde delikler olsa bile.
1999 yılında bunun ilk kanıtı yapıldı. Erik Demaine adlı genç bir profesör tarafından… Bu kanıtı merak ediyorsanız kendisinin MIT’de bu konuyla ilgili verdiği dersin tamamını ücretsiz olarak izleyebilirsiniz. Ne günlerde yaşıyoruz ama İngilizcesi ya da vakti yeterli olmayanlar için ben bu videoda zaten çok teknik ayrıntılara girmeden özetini anlatıyorum.
Katla ve Kes Teoremi 1999’da kanıtlandı ama bu teknik daha önceden de biliniyordu. Bunun yayımlanmış ilk örneği Japonya’da 1721’de basılmış bir kitapta karşımıza çıkıyor. Wakoku Chiyekurabe adlı bu kitabın anlamı matematik yarışmaları. Anlayacağınız öğrencilerin kaderi hiç değişmemiş. O zamanlar da böyle test kitaplarıyla boğuşuyorlarmış. Kitaptaki sorulardan bir tanesi kağıdı nasıl katlarsanız tek kesikte sangaibisi şekli elde edersiniz? Sangaibisi Japonların üç zirveli dağların şekline verdiği isim. Evet bunun için bile bir isimleri var. Kitapta hem bu soru hem de çözümü var.
Tarihten başka bir örnek de bayraklarla ilgili. Bilmiyorum dikkatinizi çekti mi ama yüzlerce ülkenin bayrağında bizim bayrağımız da dahil olmak üzere ortak bir şekil var: yıldız şekli. Aslında güzel bir konu bu belki ileride bu bayraklardaki yıldızlarla ilgili de bir video yaparım. Ama bugünkü konumuz bu değil. Rivayete göre Amerikan bayrağındaki yıldızların önce 6 köşeli yıldız olması düşünülmüş. Fakat 1777’de bayrağı tasarlayanlardan Betsy Ross adında bir kadın George Washington’a demiş ki biz bu yıldızları 6 değil de 5 köşeli yıldız yapalım. Böylece kumaşa bir makas atarsak yıldız şeklini elde ederiz. Tabi kadıncağız tasarlamakla kalmayıp bir de onu dikmek zorunda. Düşünsenize o zamanlar 13 tane yıldız varmış. Şimdi bu sayı 50’ye çıktı. Her bir yıldızı tek tek kesmek yerine kumaşı öyle bir katlayalım ki tek bir kesikte yıldız şeklini elde edelim demiş ve bu önerisi kabul edilmiş.
Bakın size tek kesikte yıldızı nasıl yapacağınızı göstereyim. Hem de nereden göstereyim biliyor musunuz? Houdini’nin 1922’de yazdığı bir kitaptan. Şu meşhur sihirbaz Houdini gösterilerinde bu yıldızı yaparmış zamanında. Sonra başka sihirbazlar onun bu numarasını geliştirip kağıttan başka başka şekilleri de tek kesikte yapmaya başlamışlar.
Sonra işe matematikçiler el atmış, konuyu bir teoreme dönüştürüp kanıtlamışlar ve bugüne kadar iki ayrı çözüm üretmişler. Düz iskelet yöntemi ve disk paketleme yöntemiyle artık dilediğiniz şekli katlayarak tek kesikte ortaya çıkartabiliyorsunuz. Mesela başta bahsettiğim Dr. Katie Steckles alfabedeki tüm harfleri sadece kağıtları katlayarak tek bir makas kesiğiyle yapabiliyor. Grafik tasarımcılar bu yöntemle font tasarımı bile yapmışlar.
İyi de koskoca matematikçiler niye böyle bir işle uğraşıyorlar, hatta uğraşmakla kalmayıp dünyanın en iyi üniversitelerinde bunun dersini veriyorlar diye aklınıza bir soru gelebilir. Bu sorunun en iyi cevabını muhtemelen gelecekte alacağız. Çünkü yapmaya çalıştıkları şey bir algoritma yazmak. Algoritma nedir? Bir problemin çözümünde izlenecek yol. En çok nerede kullanılır? Bilgisayarlarda. Yazılım geliştirirken. Bir bilgisayara kağıttaki bu şekli nasıl tek kesikte elde ederiz diye soramazsınız? Sorarsınız da onun cevap vermesi için yol göstermeniz gerekir. Bir algoritma yazmanız:
- Kağıdın üzerine daireler çiz
- Bu daireler birbirine dokunsun ama çakışmasın
- Daireler arasındaki boşluklar en fazla 3 ya da 4 kenarlı olsun
- Şeklin her köşesi bir dairenin merkezinde yer alsın
- Dairelerin yarıçaplarını birleştirerek katlama noktalarını bul
Tebrikler! “Disk paketleme” yöntemiyle bir algoritma geliştirdiniz. İşte bu 5 adımlı algoritmayı daha sonra hangi bilgisayar diliyle yazarsanız yazın. Hatta siz yazmasanız da olur. Önemli olan bu adımları bulmak. Problemin çözüm yolunu. Daha şimdiden telekominikasyon alanında disk paketleme algoritması kullanılmaya başlandı. Bu yöntemle daha verimli çalışan modemler yapıldı. Eğer kendinizde bu şekilde bir düşünme becerisini geliştirirseniz gezegenin en faydalı, en aranan beyinlerinden biri haline gelirsiniz. Sonra da beyaz bir kağıdın içinden kuğu gibi güzellikler çıkartırsınız…
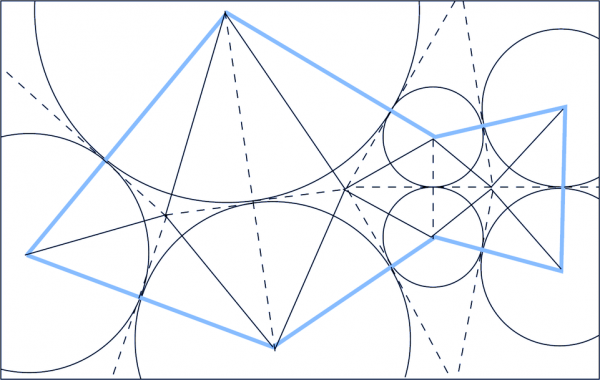
Kuğu demişken. Başta size gösterdiğim bu şekli az önce bahsettiğim algoritmayla çizebilirsiniz. Ya da videonun altında verdiğim linkten indirip bastırabilirsiniz. Sonra kesikli noktalı çizgiler tepe, sadece kesikli çizgiler de vadi olacak şekilde katlayıp, kalın çizgileri paralel hale getirirseniz tek bir makas kesiğiyle kuğu şeklini ortaya çıkartabilirsiniz.
Demek ki bize ne lazımmış? Beyaz kağıdın içindeki bu güzelliği görebilmek için sanat, ortaya çıkartabilmek için tasarım ve bu işi kurallara bağlayıp otomatik olarak üretebilmek için de bilimsel düşünce ve teknoloji.
